A matemática e os grids têm um papel muito importante no design, que permeia desde os primórdios gráficos até hoje.
Neste artigo vou trazer muitas justificações para decisões que hoje não consideramos.
Se você ainda não entende a implicação de assuntos como “o formato de uma página” e “tamanho de um bloco de texto”, esse artigo foi feito para você.
A forma da página
Tipógrafos e escribas têm configurado espaços visuais há milhares de anos, e algumas proporções foram recorrentes em seus trabalhos porque os agradavam visualmente e, em outros casos, eram confortáveis à mão.
Muitas dessas proporções são inerentes às formas geométricas simples, como triângulo equilátero, quadrado, pentágono e o hexágono.
Uma página pode ter qualquer tamanho e proporção, mas algumas dimensões são notadamente mais agradáveis para o ser humano do que outras.
E essas proporções não só agradam pessoas de séculos e países diferentes como também podem ser encontradas na natureza.
São estruturas vistas em moléculas, cristais minerais, bolhas de sabão e flores. Parece que essa beleza vai além do gosto regional ou última moda.
A aritmética e a matemática podem afastar alguns leitores, mas é inegável a participação delas na formulação de proporções e transposição de padrões da natureza para trabalhos humanos.
Proporções geométricas
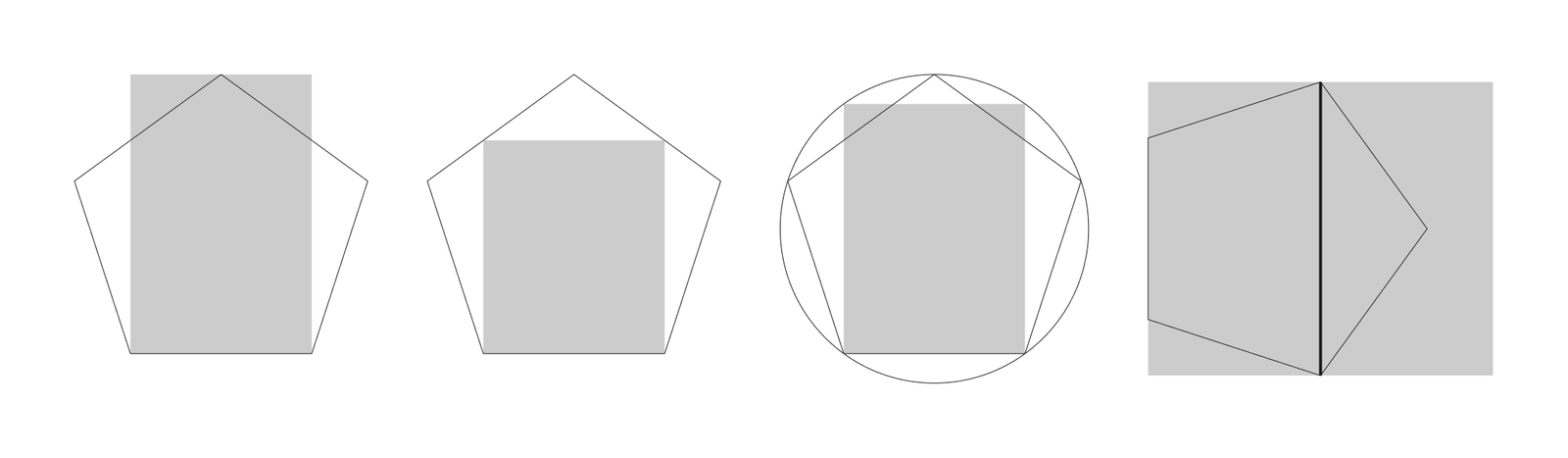
A partir de formas geométricas, conseguimos definir proporções para páginas simples e duplas:
Pentágonos
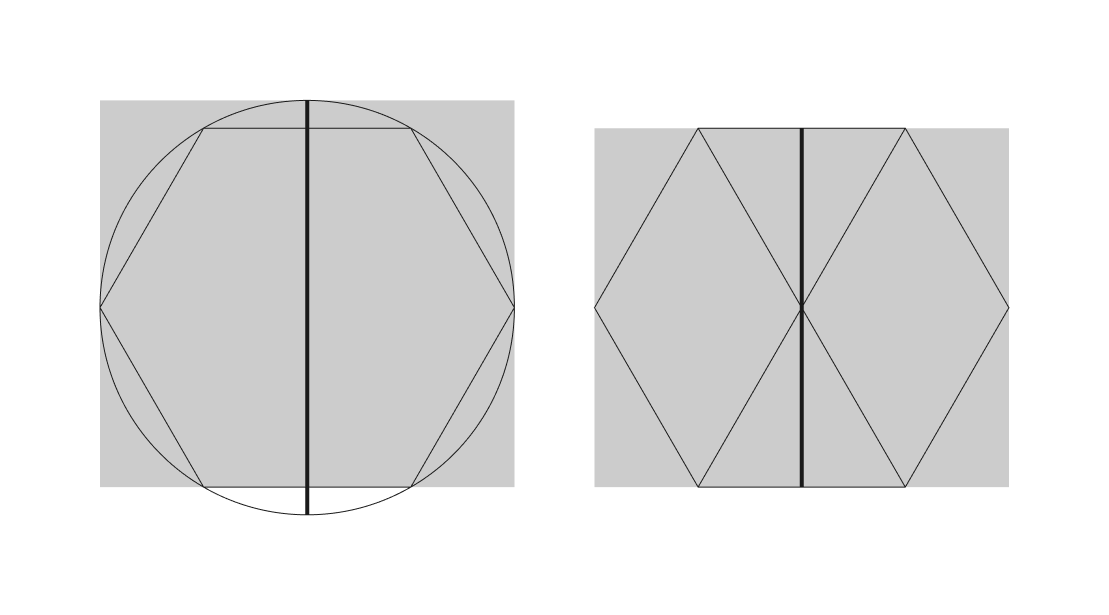
Hexágonos
Padrão ISO
Dobrar uma folha de proporção 1:√2 vai resultar em uma folha com metade do tamanho mas com as mesmas proporções.
Dobre uma folha A2 ao meio e você terá uma folha A3, dobre essa e terá uma folha A4 e assim sucessivamente. A base desse sistema é a folha A0, que tem área de 1m².
Por uma questão de conveniência, grande parte dos materiais gráficos são criados a partir da série A, que garante maior eficiência do uso do papel, já que as placas de impressão possuem o tamanho A0.
Uma vez que cada formato deriva do seu precedente, a proporção inicial 1:√2 sempre será mantida em todas as páginas do livro, independente do número de dobras feitas na composição.
Explicando
Imagine um retângulo deitado. O que o difere de um quadrado é a diferença dos lados. Logicamente, no retângulo há um lado maior e um lado menor.
Para ficar mais simples, vamos representar esses lados através de duas letras. A letra “P” representa o lado maior enquanto a letra “Q” o lado menor do retângulo.
Se dobrarmos esse retângulo ao meio a partir de um eixo vertical, isto é, dividindo “P” por 2, temos um novo retângulo de proporção Q:P/2.
Igualando essa proporção e utilizando regra de 3, chegamos a esse resultado:
Bloco de texto
Depois de definirmos a forma de uma página, é necessário reservar uma espaço de atuação para o texto, também conhecido como bloco de texto.
Faça com que a forma do bloco de texto se equilibre e contraste com o formato geral da página.
Um bloco de texto quadrado em uma página quadrada com margens iguais não é a melhor forma de encorajar a leitura.
Pois na construção de um layout, a margem possui três tarefas:
- Amarrar o bloco de texto à página;
- Emoldurar o bloco de texto;
- Proteger o bloco.
O texto precisa ser atraente para o leitor, e para isso é necessário quebrar a mesmice e procurar outro tipo de equilíbrio. Algum espaço precisa se estreitar para que outro possa se alargar. Algum espaço precisa estar vazio para que o outro possa ser cheio.
Exemplo
Abaixo temos um exemplo de bloco de texto conhecido como diagrama de Villard:
Para fazê-lo, você vai traçar diagonais no espaço total da página que irá revelar o centro. Uma nova linha partirá do ponto à esquerda-base e outra linha a partir da direita-base até o ponto superior central.
O encontro das duas diagonais revelará uma linha vertical que, conectada a partir de uma diagonal do outro ponto, vai descrever o ponto inicial do bloco de texto, que tem seu fim horizontal na primeira diagonal e altura igual ao ponto tangente de uma linha vertical com a mesma diagonal.
Conclusão
Segundo Robert Bringhurst no livro Elementos do Estilo Tipográfico “a matemática não está aí para impor trabalhos forçados a ninguém; ao contrário, seu único propósito é o prazer. Ela está aí para garantir o prazer daqueles que gostam de examinar o que estão fazendo, o que fizeram ou o que farão, talvez na esperança de fazê-lo ainda melhor”.
Não é necessário gostar ou saber matemática para fazer o que ela descreve. Quando andamos de bicicleta, por exemplo, não estamos fazendo análises matemáticas conscientes sobre o percurso.
Da mesma forma, as conchas e caracóis não precisam de tabelas logarítmicas para construir espirais logarítmicas perfeitas.
Fomos construídos para enxergar a matemática com repulsa, mas espero que através deste artigo, você amplie sua visão para a importância dela no mundo.